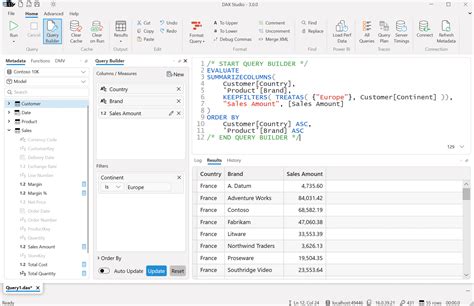
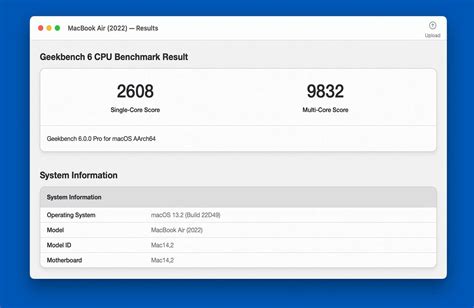
Circle theorems

Author: s | 2025-04-24

Outline. Circle Theorems. Circle Theorem 1 - Angle at the Centre; Circle Theorem 2 - Angles in a Semicircle; Circle Theorem 3 - Angles in the Same Segment

Circle theorems - Higher - AQA Circle theorems

Arc, notes study.com. The formula for finding the area of a sector is: A = (Sector Angle / 360) * (π * r^2) Using the example from slide No. 5, the radius is 4.5 inches, and the sector angle is 34 degree, you would have: A = 34 / 360 * (3.14 * 4.5^2) A = .094 * (63.585) Rounding to the nearest tenth yields: A = .1 * (63.6) A = 6.36 square inches After rounding again to the nearest tenth, the answer is: The area of the sector is 6.4 square inches. Inscribed Angles An inscribed angle is an angle formed by two chords in a circle which have a common endpoint. The formula for finding the inscribed angle is: Inscribed Angle = 1/2 * Intercepted Arc The intercepted arc is the distance of the curve formed between the two points where the chords hit the circle. Mathbits gives this example for finding an inscribed angle: An angle inscribed in a semicircle is a right angle. (This is called Thales theorem, which is named after an ancient Greek philosopher, Thales of Miletus. He was a mentor of famed Greek mathematician Pythagoras, who developed many theorems in mathematics, including several noted in this article.) Thales theorem states that if A, B, and C are distinct points on a circle where the line AC is a diameter, then the angle ∠ABC is a right angle. Since AC is the diameter, the measure of the intercepted arc is 180 degrees—or half F(x), the graph of y = f(x − h) + k is the graph of y = f(x) transformed by a horizontal shift of h units and a vertical shift of k units The y-intercept of a graph is the point where the graph crosses the y-axis, and it has an x-value of 0. Alternate Method : The y-intercept of a graph is the point where the graph crosses the y-axis, and it has coordinates (0, y). The question asks for the y-intercept of the graph of y = g(x − 3), but the given graph shows y = g(x). First plug x = 0 into y = g(x − 3). y = g(x − 3) y = g(0 − 3) Plug in x = 0 y = g(−3) Simplify Therefore, the y-intercept of the graph of y = g(x − 3) has a y-value that is equal to the value of g(−3). The function notation g(−3) means the value of the function g when x is −3. To identify the value of g(−3) from the given graph, find the y-value of the point where x = −3. The value of g(−3) is 4. Therefore, the graph of g(x − 3) has y-intercept (0, 4). Things to remember: The y-intercept of a graph is the point where the graph crosses the y-axis, and it has an x-value of 0. The function notation f(a) means the output (or value) of f(x) when the input is a. Boost Your Digital SAT Math Score We have everything you need to score a 750+! Geometry and TrigonometryThis section asks a total of 5-7 questions (15%) on area, volume, parameters of lines, angles, circles, right triangles, and right triangle trigonometry. Tricks and strategies to ace Geometry and TrigonometryAs geometry and trigonometry make up the core of this domain, familiarity with geometric rules, theorems, and trigonometry is vital. In particular, be sure you can recognize how angle values relate to each other within sets of parallel lines or triangles, noting which angles must be congruent (equivalent) or supplementary (adding up to 180 degrees). Circle theorems comprise a small portion of this section, so they do not appear on every exam. Still, many students need to familiarize themselves with how to arrive at the size and angles of a given circle, so once you're confident in the other categories, take time to memorize these applications.Geometry and Trigonometry in Math examples Question 1 Question 2 Question 3 In the figure above, line m is parallel to line n. If y = 75 and z = 50, what is the value of x ? Hint: When parallel lines are intersected by a transversal, they form pairs of corresponding angles that are congruent. Explanation First label the figure with the given information y = 75 and z = 50, as well as m || n. When parallel lines are intersected a transversal, the pairs of corresponding angles that they form are congruent (equal in measure).It is given that lines m

Circle Theorems - Learn all Circle Theorems for Class

What is FX Draw? FX Draw draws any diagram a secondary mathematics teacher (or student) might need and lets you place publication quality graphics into documents, web pages and presentations quickly and easily. You can also use FX Draw with interactive whiteboards and data projectors to produce an interactive and intuitive teaching environment. What can FX Draw Do?Click on the headings to see an example of the sort of images FX Draw can draw. Each of these images was drawn quickly and easily usingFX Draw's built-in tools. Function Graphs Cartesian Polar Graphs Parametric Conic Sections Implicitly Defined Functions Shaded Integrals Integral Approximations Inequalities Normal Distribution Curves Number Lines Derivative Curves Tangent Lines Implicitly Defined Inequations Points Vectors Plot As Points Complex Numbers and Equations Tables of Values Greatest Integer Function Piecewise Defined Functions Slope Fields and 1st Order Differential Equations Families of Curves Animations Geometric Diagrams Parallel Line Theorems Circle Geometry Pythagoras Geometric Constructions Regular Polygons Angle Marks I like FX Draw very much - it's a real mathematician's tool - and I am happy that I could do some beta testing work. The new version is really good. Congratulations! J Kamerling - Netherlands FX Draw provides over 50 specialised mathematical drawing tools and over 500 pre drawn objects. The only limit to what FX Draw can draw is your imagination!. Outline. Circle Theorems. Circle Theorem 1 - Angle at the Centre; Circle Theorem 2 - Angles in a Semicircle; Circle Theorem 3 - Angles in the Same Segment Outline. Circle Theorems. Circle Theorem 1 - Angle at the Centre; Circle Theorem 2 - Angles in a Semicircle; Circle Theorem 3 - Angles in the Same Segment

Circle theorems - Higher - Edexcel Circle theorems - Higher

Instructions: Use this step-by-step Total Probability Rules calculator to compute the probability of an event \(A\), when you know the conditional probabilities of \(A\) with respect to a partition of events \(B_i\). Please type in the conditional probabilities of A with respect to the other events, and optionally, indicate the name of the conditioning events in the form below: More About the Law of Total Probability The Law of Total Probability is one of the most important theorems in basic Probability theory. It is a result that gives a clear link of how the probability of an event \(A\) is composed of these parts based on conditional events that form up the "total" of the probability of the event \(A\). Now, in mathematical terms, let \(\left\{B\right\}_{i=1}^n\) be a partition of the sample space, and let \(A\) be an event. Then, the probability of the event A can be partitioned in the following way. \[\Pr(A) = \Pr(A | B_1) \Pr(B_1) + \Pr(A | B_2) \Pr(B_2) + ... + \Pr(A | B_n) \Pr(B_n)\] The Total Probability Rule is a pivotal theorem in Probability and Statistics, and it is the foundation of other crucial theorems such as the Theorem of Bayes . This website uses cookies to improve your experience. We'll assume you're ok with this, but you can opt-out if you wish. Accept Read More A trapezoid is a quadrilateral with at least one pair of parallel sides. The median of a trapezoid is a segment joining the midpoints of the legs of the trapezoid. (At the right, is the median fortrapezoid ABCD.) The theorems will be stated in "if ...then" form. Both the theorem and its converse (where you swap the "if" and "then" expressions) will be examined. Click in the charts below to see each proof.While one method of proof will be shown, other methods are also possible. Definition and Theorems pertaining to a trapezoid: DEFINITION: A trapezoid is a quadrilateral with at least one pair of parallel sides. THEOREM: The median of a trapezoid is parallel to the bases and half the sum of the lengths of the bases. ISOSCELES TRAPEZOID A isosceles trapezoid is a trapezoid with congruent base angles. Note: The definition of an isosceles triangle states that the triangle has two congruent "sides". But the definition of isosceles trapezoid stated above, mentions congruent base "angles", not sides (or legs). Why not? If an "inclusive" isosceles trapezoid is defined to be "a trapezoid with congruent legs", a parallelogram will be an isosceles trapezoid. If this occurs, the other properties that an isosceles trapezoid can possess can no longer hold, since they will not be true for a parallelogram. If, however, we define an isosceles trapezoid to be a "trapezoid with congruent base angles", the legs can be proven congruent, a parallelogram will NOT be an isosceles trapezoid, and all of

Circle theorems - Higher - OCR Circle theorems - Higher

The commonly known properties of an isosceles trapezoid will remain true. Definition and Theorems pertaining to an isosceles trapezoid: DEFINITION: An isosceles trapezoid is a trapezoid with congruent base angles. THEOREM: If a quadrilateral (with one set of parallel sides) is an isosceles trapezoid, its legs are congruent. THEOREM: If a quadrilateral is an isosceles trapezoid, the diagonals are congruent. THEOREM: (converse) If a trapezoid has congruent diagonals, it is an isosceles trapezoid. THEOREM: If a quadrilateral is an isosceles trapezoid, the opposite angles are supplementary. THEOREM: (converse) If a trapezoid has its opposite angles supplementary, it is an isosceles trapezoid. KITE A kite is a quadrilateral whose four sides are drawn such that there are two distinct sets of adjacent, congruent sides. Note: Kites discussed on this page are convex kites. Definition and Theorems pertaining to a kite: DEFINITION: A kite is a quadrilateral whose four sides are drawn such that there are two distinct sets of adjacent, congruent sides. THEOREM: If a quadrilateral is a kite, the diagonals are perpendicular. THEOREM: If a quadrilateral is a kite, it has one pair of opposite angles congruent. THEOREM: If a quadrilateral is a kite, it has one diagonal forming two isosceles triangles. THEOREM: If a quadrilateral is a kite, it has one diagonal forming two congruent triangles. THEOREM: If a quadrilateral is a kite, it has one diagonal that bisects a pair of opposite angles. THEOREM: If a quadrilateral is a kite, it has one diagonal that bisects the other

CIRCLE THEOREMS: How to solve different Circle theorem

Says that his father was Phidias, an astronomer.Except for a period spent in Alexandria, Egypt, where he studied under the followers of the mathematician Euclid, Archimedes spent his life in Syracuse. According to Plutarch, the ancient Greek historian and biographer, Archimedes was a distant cousin of Hiero II, the ruler of Syracuse. Hiero’s long reign was a period of peace and stability in Syracuse, and gave Archimedes the opportunity to pursue his work in peace. Hiero often turned to Archimedes for advice on military and other matters.Archimedes is regarded as the greatest mathematician and scientist of his age, though only a few of his writings have survived into modern times. According to the Encyclopaedia Britannica, there are only nine known extant treatises in Greek by Archimedes.Of these treatises, five are of particular interest:On the Sphere and Cylinder (two volumes): this contains his discovery that the volume of a sphere is two-thirds that of the cylinder in which it is inscribed, and that the surface area of a sphere is four times that of its greatest circle.On the Measurement of the Circle: a short work which contains his approximation for the value of Pi. Archimedes showed that Pi lies between 223/71 and 22/7. The latter value was used throughout the Middle Ages and it is still used today when a rough calculation is required. This work also contains accurate approximations of the square roots of various numbers.On Floating Bodies (two volumes): this is the first known work in hydrostatics (the study of liquids at rest), a branch of science of which Archimedes is considered the founder. This is the work that leads to the Archimedes Principle, which states that a body partially or completely immersed in a fluid is buoyed up by a force equal to the weight of the fluid displaced by the body.The Method of Mechanical Theorems: this describes the process of discovery in mathematics. In it, Archimedes describes some of the ‘mechanical’ techniques he used to arrive at the values he proved mathematically in On the Sphere and Cylinder.The Sand Reckoner: this is a small work, written for the layman. It deals with the inadequacies of the Greek numerical notation system, by showing how to express a very large number – the number of grains of sand that it would take to fill the universe. In doing this, he, in effect established a place-value system, with a base. Outline. Circle Theorems. Circle Theorem 1 - Angle at the Centre; Circle Theorem 2 - Angles in a Semicircle; Circle Theorem 3 - Angles in the Same Segment Outline. Circle Theorems. Circle Theorem 1 - Angle at the Centre; Circle Theorem 2 - Angles in a Semicircle; Circle Theorem 3 - Angles in the Same Segment

Circle theorems - Higher - OCR Circle theorems - Higher - BBC

Of group theory and its applications in various mathematical fields. 5. The four color theoremA four-colored map.Problem:The four color theorem tackles an intriguing question related to topology and stands as one of the first significant theorems proved by a computer. It states that any map in a plane can be colored using four colors so that no two adjacent regions share the same color while using the fewest possible colors. Adjacent, in this context, means that two regions share a common boundary curve segment, not merely a corner where three or more regions meet.The theorem doesn’t focus on the artistic aspect of map coloring but rather on the fundamental mathematical principles that underlie it.Solution: The solution to this theorem arrived in 1976, thanks to the combined efforts of mathematicians Kenneth Appel and Wolfgang Haken. However, the proof was not widely accepted due to the infeasibility of checking it by hand.Appel and Haken’s achievement confirmed that any map, regardless of its complexity, can be colored with just four colors such that no two neighboring regions share the same color. While the idea seems simple, proving it rigorously was complex and time-consuming.To address any lingering skepticism about the Appel–Haken proof, a more accessible proof using similar principles and still utilizing computer assistance was presented in 1997 by Robertson, Sanders, Seymour, and Thomas. Additionally, in 2005, Georges Gonthier achieved a proof of the theorem using general-purpose theorem-proving software, reinforcing the credibility of the four color theorem.This theorem is not actually used in map-making but has far-reaching implications in various fields, from graph theory to computer science, where it finds applications in scheduling, circuit design, and optimization problems.6. Gödel’s incompleteness theoremsGödel published his findings in a book.Problem:Gödel’s incompleteness theorems, formulated by Austrian mathematician Kurt Gödel in the 20th century, delve into the mysteries of formal systems and their inherent limitations. In mathematics, a formal system has a structured and well-defined framework or language that comprises a set of symbols, rules, and axioms employed for representing and manipulating mathematical or logical expressions.Gödel’s first incompleteness theorem explores a fundamental question: In any consistent formal system, are